はじめに

現代の人工知能（AI）、特に大規模言語モデル（LLM）は、人間のようなテキスト生成や対話能力を持つ一方で、その学習には膨大な計算資源を必要とします。この計算の壁を乗り越える鍵となるのが「並列処理（Parallel Processing）」技術です。本シリーズでは、先進的なLLMであるDeepSeekの技術を解説しています。Part1ではモデルアーキテクチャに焦点を当てましたが、Part2となる本記事では、DeepSeekがいかにして巨大なモデルを効率的に学習させているのか、その心臓部とも言える並列処理技術について、背景となる理論から具体的な手法まで、わかりやすく解き明かしていきます。

なぜ「並列処理」の前に「誤差逆伝播法」？

並列処理の詳細に入る前に、ニューラルネットワークの学習における基本的なアルゴリズム「バックプロパゲーション（誤差逆伝播法）」について理解しておく必要があります。なぜなら、この誤差逆伝播法の計算負荷が非常に高く、それをいかに効率化するか（＝並列化するか）がLLM開発の大きな課題だからです。誤差逆伝播法は、モデルの予測（出力）と正解（教師データ）のズレ（誤差）を計算し、その誤差をネットワークの層を遡って伝えることで、各接続の重みを調整し、モデルの精度を高めていく手法です。

ニューラルネットワークの数式表現

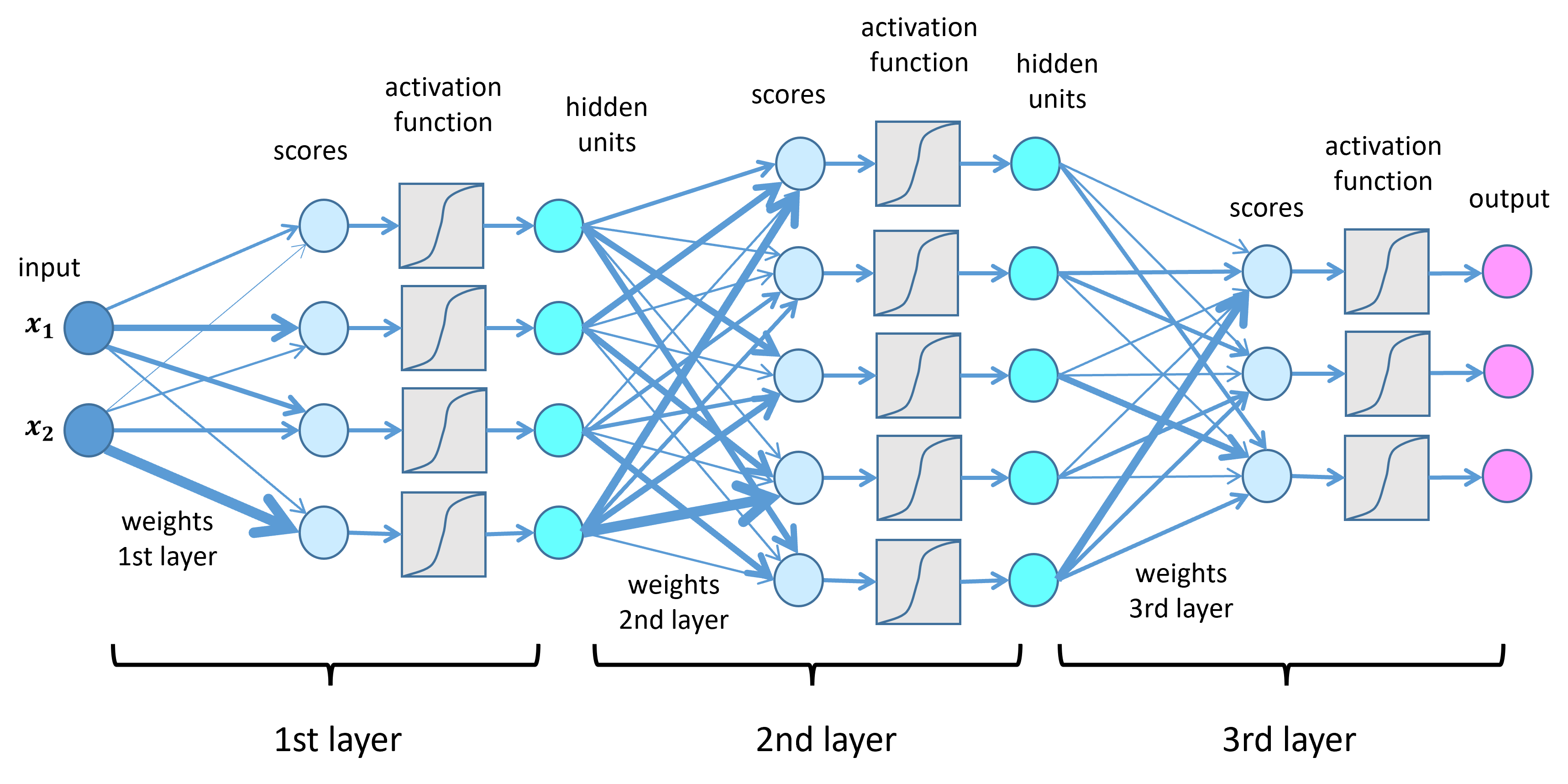
ニューラルネットワークはよくノードと矢印で図示されますが、行列とベクトルを用いると、その計算を簡潔な数式で表現できます。

ある層が、前の層から n 個の入力値を受け取り、m 個のノード（ニューロン）で構成されているとします。入力値を要素とする n 次元のベクトルを \(\mathbf{z}^{(l-1)}\)（前の層の出力、または最初の層の場合は入力データ \(\mathbf{x}\)）、この層の出力を m 次元ベクトル \(\mathbf{z}^{(l)}\) とします。各接続の重みは \(m \times n\) 行列 \(W^{(l)}\) で表され、バイアス項ベクトルを \(\mathbf{b}^{(l)}\) (m次元) とすると、この層の計算は以下のように表せます。

まず、重み付きの合計とバイアスを加算します。

\[\mathbf{u}^{(l)} = W^{(l)} \mathbf{z}^{(l-1)} + \mathbf{b}^{(l)}\]

次に、計算結果 \(\mathbf{u}^{(l)}\) の各要素に活性化関数 f を適用し、この層の出力 \(\mathbf{z}^{(l)}\) を得ます。

\[\mathbf{z}^{(l)} = f(\mathbf{u}^{(l)})\]

ここで、重み行列 \(W^{(l)}\) は具体的に以下のような形をしています（\(w_{ij}^{(l)}\) は l 層目の i 番目のノードと l-1 層目の j 番目のノード間の重み）。

\[ W^{(l)} = \begin{pmatrix} w_{11}^{(l)} & \cdots & w_{1j}^{(l)} & \cdots & w_{1n}^{(l)} \\ \vdots & \ddots & \vdots & \ddots & \vdots \\ w_{i1}^{(l)} & \cdots & w_{ij}^{(l)} & \cdots & w_{in}^{(l)} \\ \vdots & \ddots & \vdots & \ddots & \vdots \\ w_{m1}^{(l)} & \cdots & w_{mj}^{(l)} & \cdots & w_{mn}^{(l)} \end{pmatrix} \]

ネットワーク全体が L 層で構成される場合、入力 \(\mathbf{x} = \mathbf{z}^{(0)}\) から始まり、\(l=1, 2, \dots, L\) と順に計算を進め、最終的な出力 \(\mathbf{y} = \mathbf{z}^{(L)}\) を得ます。

誤差逆伝播法の詳説

学習の目標は、モデルの出力 \(\mathbf{y}\) が教師データ \(\mathbf{d}\) にできるだけ近くなるように、重み \(W^{(l)}\) やバイアス \(\mathbf{b}^{(l)}\) を調整することです。その「近さ」を測る指標として誤差関数 E を定義します。ここでは一般的な二乗誤差を考えます。

\[E = \frac{1}{2} \|\mathbf{y}-\mathbf{d}\|^2\]

この誤差 \(E\) を最小化することが学習の目的です。誤差逆伝播法は、この \(E\) を各パラメータ（\(w_{ij}^{(l)}\) や \(b_i^{(l)}\)）で偏微分した値（勾配）を計算し、その勾配を利用してパラメータを更新する手法です。

パラメータ \(w_{ij}^{(l)}\) の更新量は、勾配に学習率 \(\eta\) （イータ：更新幅を調整する係数）を乗じた値の逆方向に設定されます。

\[\Delta w_{ij}^{(l)} = -\eta \frac{\partial E}{\partial w_{ij}^{(l)}}\]

（バイアス \(\mathbf{b}^{(l)}\) についても同様です。）

勾配 \(\frac{\partial E}{\partial w_{ij}^{(l)}}\) を計算するのが核心部ですが、\(w_{ij}^{(l)}\) の変更は後続のすべての層に影響を与え、最終的な誤差 E に複雑な影響を及ぼします。そこで誤差逆伝播法では、出力層から入力層に向かって逆方向に計算を進めることで、この複雑な計算を効率的に行います。この計算には、微分の連鎖律（Chain Rule）が用いられます。

連鎖律（簡単に）

y が u の関数で、u が x の関数（y = f(u), u = g(x)）のとき、y を x で微分するには \(\frac{dy}{dx} = \frac{dy}{du} \frac{du}{dx}\) と計算できます。多変数の場合も同様に、ある変数の変化が他の変数を介して最終的な値にどう影響するかを連鎖的に計算できます。

誤差逆伝播法の計算ステップ

計算を簡単にするため、ここでは出力層（L 層目）の活性化関数を恒等関数 \(f(x)=x\) と仮定します（つまり \(\mathbf{z}^{(L)} = \mathbf{u}^{(L)}\) なので \(\mathbf{y} = \mathbf{u}^{(L)}\)）。

出力層 (l=L) の誤差計算:

まず、誤差 E を \(\mathbf{u}^{(L)}\) の各要素で偏微分した値 \(\boldsymbol{\delta}^{(L)}\) を計算します。これは「誤差信号」とも呼ばれます。 \(\boldsymbol{\delta}^{(L)} = \frac{\partial E}{\partial \mathbf{u}^{(L)}} = \frac{\partial E}{\partial \mathbf{y}} \frac{\partial \mathbf{y}}{\partial \mathbf{u}^{(L)}}\) ここで \(\frac{\partial E}{\partial \mathbf{y}} = \mathbf{y} - \mathbf{d}\) であり、\(\frac{\partial \mathbf{y}}{\partial \mathbf{u}^{(L)}} = \mathbf{1}\) (要素ごとの微分なので、活性化関数が恒等関数の場合は1) です。したがって、 \(\boldsymbol{\delta}^{(L)} = \mathbf{y} - \mathbf{d}\) となります。これはまさにモデルの出力と教師データの差（誤差）そのものです。

出力層の勾配計算:

\(\boldsymbol{\delta}^{(L)}\) を使うと、出力層の重み \(W^{(L)}\) に関する勾配は次のように計算できます。 \(\frac{\partial E}{\partial w_{ij}^{(L)}} = \frac{\partial E}{\partial u_i^{(L)}} \frac{\partial u_i^{(L)}}{\partial w_{ij}^{(L)}} = \delta_i^{(L)} z_j^{(L-1)}\) （\(u_i^{(L)} = \sum_k w_{ik}^{(L)} z_k^{(L-1)} + b_i^{(L)}\) なので \(\frac{\partial u_i^{(L)}}{\partial w_{ij}^{(L)}} = z_j^{(L-1)}\)） 行列形式で書くと \(\frac{\partial E}{\partial W^{(L)}} = \boldsymbol{\delta}^{(L)} (\mathbf{z}^{(L-1)})^T\) となります。

中間層 (l < L) の誤差計算:

ある層 l の誤差信号 \(\boldsymbol{\delta}^{(l)}\) は、一つ先の層 l+1 の誤差信号 \(\boldsymbol{\delta}^{(l+1)}\) を使って逆向きに計算できます。 \(\boldsymbol{\delta}^{(l)} = \frac{\partial E}{\partial \mathbf{u}^{(l)}} = \frac{\partial E}{\partial \mathbf{u}^{(l+1)}} \frac{\partial \mathbf{u}^{(l+1)}}{\partial \mathbf{z}^{(l)}} \frac{\partial \mathbf{z}^{(l)}}{\partial \mathbf{u}^{(l)}}\) 計算すると、以下のようになります。（\(\odot\) は要素ごとの積を表します）

\[\boldsymbol{\delta}^{(l)} = \left( (W^{(l+1)})^T \boldsymbol{\delta}^{(l+1)} \right) \odot f'(\mathbf{u}^{(l)})\]

ここで \(f'\) は活性化関数 \(f\) の導関数です。この式により、出力層の \(\boldsymbol{\delta}^{(L)}\) から始めて、\(\boldsymbol{\delta}^{(L-1)}, \boldsymbol{\delta}^{(L-2)}, ..., \boldsymbol{\delta}^{(1)}\) と順に計算できます。

中間層の勾配計算:

\(\boldsymbol{\delta}^{(l)}\) が計算できれば、その層の重み \(W^{(l)}\) の勾配も出力層と同様に計算できます。 \(\frac{\partial E}{\partial W^{(l)}} = \boldsymbol{\delta}^{(l)} (\mathbf{z}^{(l-1)})^T\)

このように、誤差逆伝播法では、まず順方向（Forward Pass）で各層の出力 \(\mathbf{z}^{(l)}\) と最終出力 \(\mathbf{y}\) を計算し、次に逆方向（Backward Pass）で誤差信号 \(\boldsymbol{\delta}^{(l)}\) と勾配 \(\frac{\partial E}{\partial W^{(l)}}\) を計算します。

この一連の計算、特に巨大な行列演算は、LLMのような大規模モデルでは膨大な計算量となります。1回の学習（全データに対する更新）でさえ非常に時間がかかるため、並列処理によって計算を高速化することが不可欠なのです。

3D並列処理とは？

DeepSeekのような最先端のLLMは、学習を高速化し、巨大なモデルを扱えるようにするために「3D並列処理」と呼ばれる高度な技術を採用しています。これは、以下の3つの異なる並列化戦略を巧みに組み合わせるアプローチです。

• データ並列（Data Parallelism）： データを分割し、複数のGPUで同時に処理する。
• モデル並列（Model Parallelism）： モデル自体を分割し、複数のGPUで分担して計算する。
• パイプライン並列（Pipeline Parallelism）： モデルの層を流れ作業のように複数のGPUで処理する。

これらの手法を組み合わせることで、単一の手法だけでは得られない高い効率とスケーラビリティを実現します。それぞれの方法について詳しく見ていきましょう。

データ並列（Data Parallelism）

データ並列は、最も一般的で直感的な並列化手法です。

仕組み：

同じモデルの完全なコピーを複数のGPU（ワーカー）に配置します。学習データを複数のミニバッチに分割し、各GPUがそれぞれ異なるミニバッチを使ってモデルの学習（順伝播、誤差計算、逆伝播による勾配計算）を並行して行います。

勾配の集約：

各GPUで計算された勾配は、すべてのGPU間で集約され（通常は平均を取る）、その平均勾配を使って全GPU上のモデルパラメータが一斉に更新されます。これにより、実質的により大きなバッチサイズで学習しているのと同じ効果が得られ、学習が安定しやすくなります。

利点：

実装が比較的容易で、GPU数を増やすほど学習速度を（理想的には線形に）向上させることができます。

課題：

各GPUがモデル全体のコピーと、学習状態（パラメータ、勾配、オプティマイザ状態）を保持する必要があるため、モデルが巨大になるとGPUメモリが不足しやすくなります。

メモリ効率化： ZeRO (Zero Redundancy Optimizer)

データ並列のメモリ課題を解決するために開発されたのが ZeRO です。特にDeepSeekが採用する ZeRO-1 は、メモリ消費の大きな要因であるオプティマイザ状態 (Optimizer States) に着目します。

オプティマイザ状態とは？

勾配をそのまま使ってパラメータを更新する単純な方法（SGD）もありますが、現在主流のAdamなどの高機能なオプティマイザは、過去の勾配情報（モーメントや分散など）を保持し、それを利用してより効率的にパラメータを更新します。この保持される情報がオプティマイザ状態です。

メモリ消費の内訳（例）：

モデルパラメータを16bit浮動小数点数（FP16, 2バイト）、勾配もFP16 (2バイト) で保持する場合でも、Adamオプティマイザは通常、パラメータごとに元のパラメータのコピー（FP32, 4バイト）、モーメント（FP32, 4バイト）、分散（FP32, 4バイト）の計12バイトをFP32で保持します。合計すると、パラメータ1つあたり 2 + 2 + 12 = 16 バイトものメモリが必要になります。

ZeRO-1 のアプローチ：

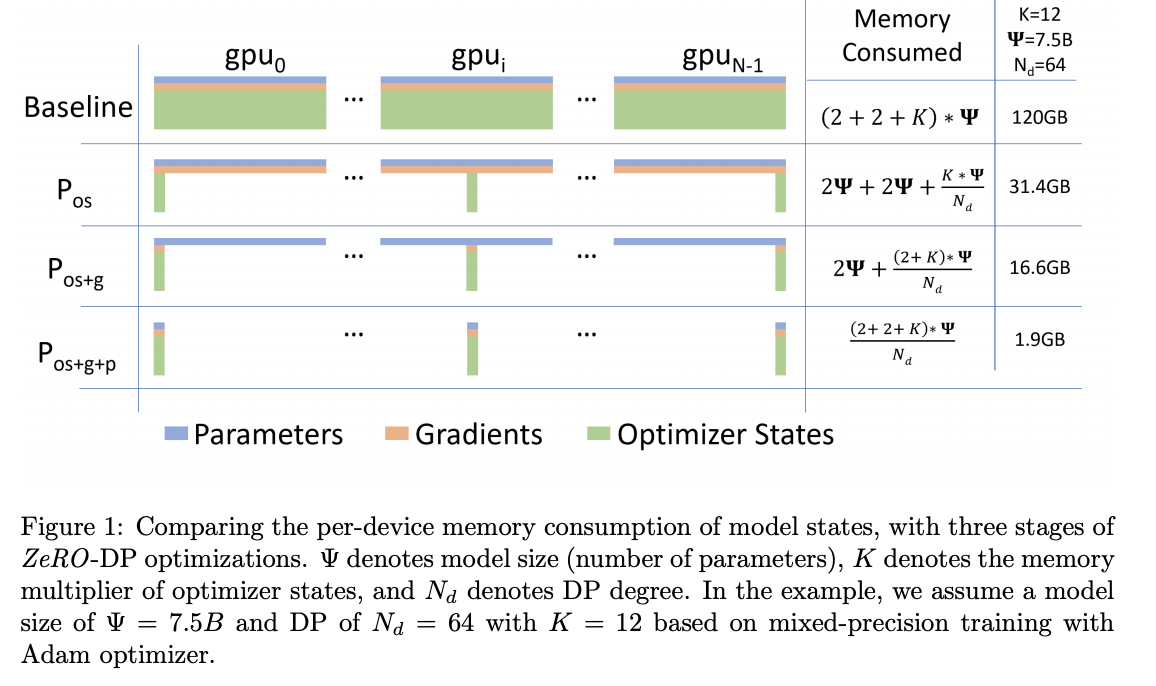
このメモリ消費の大部分（例では16バイト中12バイト）を占めるオプティマイザ状態を、各GPUで重複して持つのではなく、全GPUに分割して保持します（シャーディング）。パラメータ更新時には、必要なオプティマイザ状態を持つGPUから通信で取得します。これにより、各GPUが必要とするメモリ量を大幅に削減でき、より大きなモデルをデータ並列で学習させることが可能になります。

（補足：ZeROにはさらに進んだ ZeRO-2（勾配も分割）、ZeRO-3（パラメータも分割）がありますが、DeepSeekではZeRO-1が使われていると述べられています。）

モデル並列（Model Parallelism）

モデル並列は、モデル自体が単一GPUのメモリに収まらないほど巨大な場合に不可欠な技術です。

仕組み：

ニューラルネットワークの各層、あるいは層内部の計算（例えば巨大な行列演算）を複数のGPUに分割して割り当てます。各GPUはモデルの一部分のみを担当します。

テンソル並列（Tensor Parallelism）：

層内の行列演算 (Wx) を分割する方式です。例えば、行列 W を列方向や行方向に分割し、それぞれの部分行列と入力ベクトル（またはその一部）の計算を異なるGPUで行い、結果を集約します。TransformerモデルのAttention機構やFFN（Feed Forward Network）層など、特定の計算パターンに対して効果的です。

利点：

単一GPUのメモリ制限を超える超巨大モデルの学習を可能にします。

課題：

分割された部分計算の結果をGPU間で頻繁に通信する必要があり、通信オーバーヘッドが性能のボトルネックになりやすいです。また、どのようにモデルを分割するかが複雑になる場合があります。

パイプライン並列（Pipeline Parallelism）

パイプライン並列は、モデルの層（ステージ）を複数のGPUに割り当て、データがGPU間を流れ作業のように処理される方式です。モデル並列の一種とも考えられますが、特に層単位での分割と順次処理に焦点を当てています。

仕組み：

モデルを複数の連続したステージ（通常は複数の層）に分割し、各ステージを異なるGPUに割り当てます。入力データ（ミニバッチ）は最初のステージ（GPU 1）に入力され、その処理結果が次のステージ（GPU 2）に送られ…と、パイプラインのようにデータが流れていきます。

課題：バブル（Bubble）の発生

単純なパイプラインでは、最初のミニバッチが最後のステージに到達するまで、後段のGPUは待機状態になります（Forward Bubble）。

同様に、逆伝播時も、最後のミニバッチの勾配が最初のステージに戻ってくるまで、前段のGPUは待機状態になります（Backward Bubble）。

このGPUが遊んでいる時間（バブル）が、パイプラインの効率を低下させます。

バブル削減のための工夫

このバブル問題を軽減・解消するために、様々なアルゴリズムが考案されてきました。

GPipe:

データをさらに小さなマイクロバッチに分割し、パイプラインに連続的に投入します。あるGPUがマイクロバッチ k の順伝播を終えたら、すぐにマイクロバッチ k+1 の順伝播を開始することで、GPUの遊休時間を減らします。ただし、全マイクロバッチの順伝播が終わってから逆伝播が始まるため、アクティベーション（中間出力）をメモリに保持しておく必要があります。

PipeDream (1F1B スケジューリング):

順伝播（Forward）と逆伝播（Backward）をより密接に組み合わせます。あるマイクロバッチの順伝播が完了したGPUは、後続のマイクロバッチの順伝播だけでなく、先行するマイクロバッチの逆伝播も担当できるようにスケジューリングします（例：マイクロバッチ k の順伝播後、マイクロバッチ k-N の逆伝播を行う）。これにより、アクティベーションの保持期間が短くなり、メモリ効率が向上します。また、バブルも削減されます。

Zero Bubble (ZB):

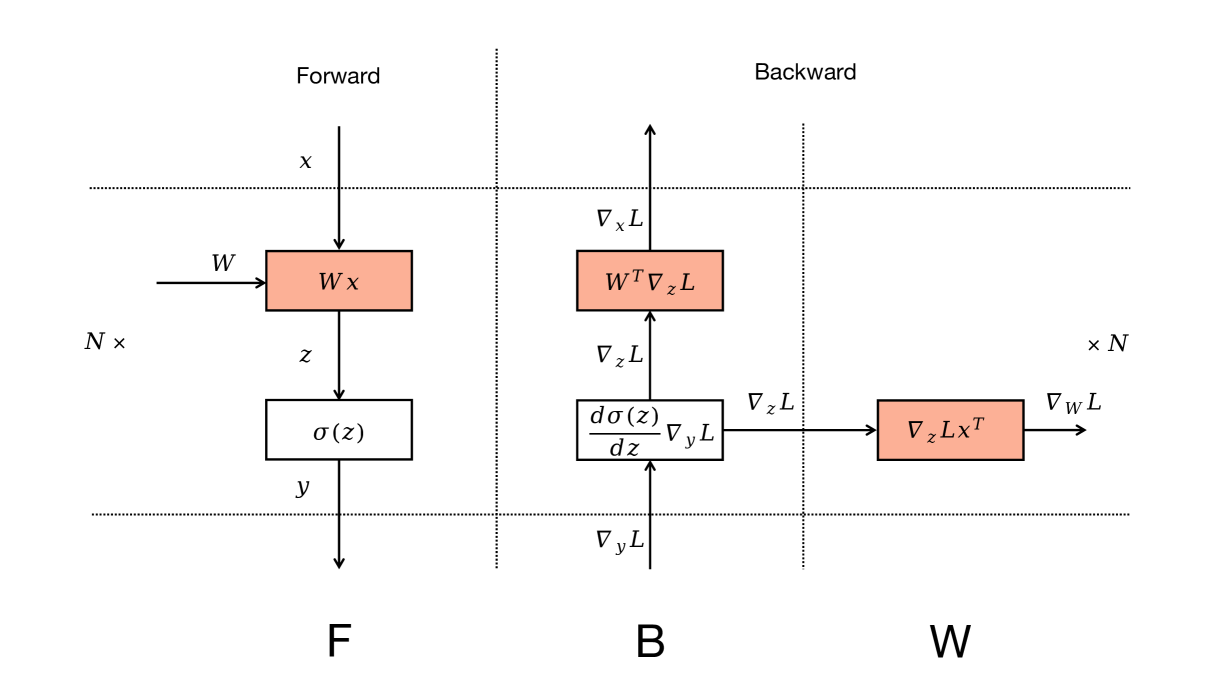
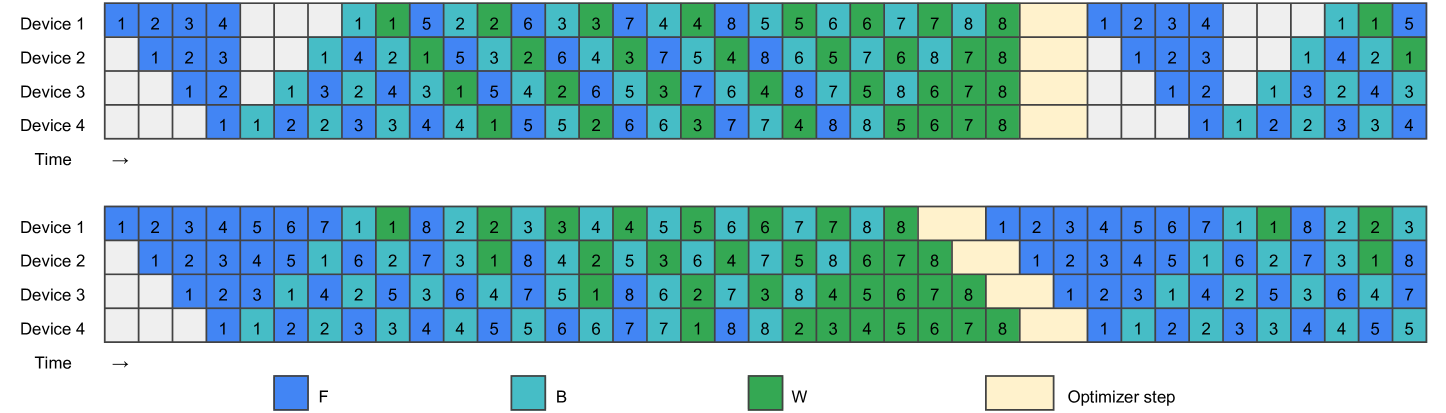
逆伝播における勾配計算とパラメータ更新を分離します。逆伝播で必要なのは、前の層に伝える誤差信号（\(\boldsymbol{\delta}^{(l)}\) の計算に必要な \((W^{(l+1)})^T \boldsymbol{\delta}^{(l+1)}\)）であり、その層自身のパラメータ更新（\(\Delta W^{(l)}\) の計算と適用）は後回しにできます。この性質を利用し、誤差信号の計算を優先して逆伝播を進め、GPUが空いた時間（本来バブルが発生する時間）を利用してパラメータ更新を行うことで、バブルの完全な排除を目指します。

DualPipe（DeepSeek V3）:

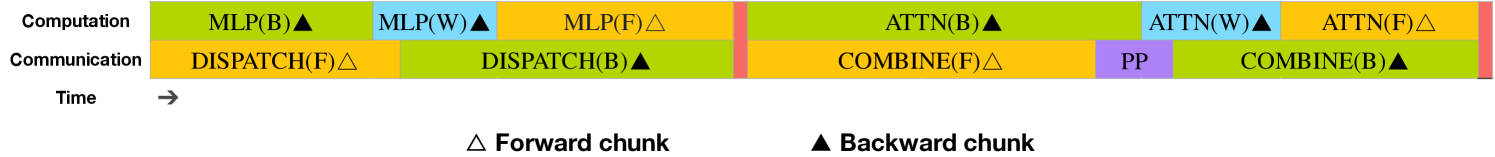
DeepSeekが開発した独自技術です。Zero Bubble の考え方をさらに推し進め、計算と通信のオーバーラップを最大化します。GPUが計算を行っている間に、バックグラウンドで他のGPUとの間で必要なデータ（アクティベーションや勾配など）を送受信します。これにより、通信にかかる待ち時間を計算処理で「隠蔽」し、パイプライン全体の効率を極限まで高めることを目指します。具体的には、あるGPUが特定のマイクロバッチの順伝播計算、別のマイクロバッチの逆伝播（誤差計算）、さらに別のマイクロバッチのパラメータ更新を、通信と並行して同時に行うような高度なスケジューリングを実現していると考えられます。

まとめ

DeepSeekは、超巨大AIモデルの効率的な学習を実現するために、洗練された3D並列処理技術を駆使しています。

• データ並列: ZeRO-1を活用し、各GPUのメモリ負担を軽減しつつ、処理速度を向上させます。
• モデル並列: 単一GPUに収まらない巨大モデルを分割し、複数のGPUで計算を分担します。
• パイプライン並列: 独自技術「DualPipe」により、計算と通信を高度にオーバーラップさせ、パイプラインの「バブル」を最小化し、GPUの稼働率を最大限に高めます。

これらの技術を組み合わせることで、DeepSeekは計算資源の制約を乗り越え、高性能なLLMの開発を可能にしています。AI、特にLLMのさらなる進化には、このような並列処理技術の発展が不可欠と言えるでしょう。

次回、Part3では「DeepSeekで扱われている強化学習」について解説します。LLMの性能をさらに引き出すための重要な技術ですので、ご期待ください。