はじめに

ソフトウェア開発の世界では、プロジェクトの目的や性質、規模、そしてチームのスキルや経験によって、最適な開発アプローチとライフサイクルを選択することが重要です。従来から主流を占めてきたウォーターフォール型開発は、各工程を順番に進めていくため、計画が立てやすく進捗管理がしやすい反面、一度開発が進んでしまうと、要件の変更に柔軟に対応することが難しいという側面も持ち合わせています。

一方、近年注目を集めているアジャイル型開発は、短いサイクルで開発とテストを繰り返しながら、柔軟に要件変更に対応していくアプローチです。特に、要件や要求が変化しやすいプロジェクトや、市場のトレンドに迅速に対応する必要のあるプロジェクトにおいて、その真価を発揮します。

予測型、漸進型、反復型、アジャイル型といった様々な開発アプローチとライフサイクルが存在しますが、これらはそれぞれにメリット・デメリットがあり、プロジェクトの特性に合わせて最適なものを選択することが重要です。実際のプロジェクトでは、これらの開発アプローチとライフサイクルは連続性を持ち、プロジェクトの特性をよく見て、うまくミックスさせて、開発アプローチとライフサイクルを組み合わせていくことが重要となります。

1. 開発アプローチとライフサイクル

1.1 開発アプローチとライフサイクルの種類

ソフトウェア開発には、予測型、漸進型、反復型、アジャイル型といった様々な開発アプローチとライフサイクルが存在します。これらはそれぞれにメリット・デメリットがあり、プロジェクトの特性に合わせて最適なものを選択することが重要です。

1.1.1 予測型

予測型開発は、ウォーターフォール型開発とも呼ばれ、要件定義、設計、実装、テスト、リリースといった工程を順番に進めていく、非常に伝統的な手法です。全体計画を最初に立てて進めるため、システムを発注する顧客側からすると、予算やスケジュールの見通しが立てやすいというメリットがあります。各工程の成果物を明確に定義し、計画に沿って進めていくため、進捗管理が容易であり、プロジェクト全体の計画が見通しやすいため、予算やスケジュールの管理がしやすいというメリットがあります。

一方、予測型開発は、要件定義の段階で全ての要件を確定させる必要があるため、要件変更に柔軟に対応することが難しいというデメリットがあります。また、開発の後半にならないと実際に動作するシステムを確認できないため、初期段階で発生した問題の影響が大きくなり、手戻りが発生しやすいというリスクも孕んでいます。成功率が低いというデメリットも挙げられています。

1.1.2 漸進型

漸進型開発は、予測型開発を細切れにしたような手法で、要件の変更程度は低いものの、デリバリー頻度を高くしたい場合に適しています。価値を生み出す成果物のサブセット、つまり成果物の一部や一部機能ごとに成果物を一つずつデリバリーしていくようなものです。話を単純化すると、この一つずつのサブセットのことを**インクリメント（増分）**と言ったりします。

この漸進型開発を採用する場合は、例えば、予測型開発では将来が予測しにくい場合や、顧客が一部の機能をできるだけ早く利用開始したい場合などに適しています。一方、一度納品したサブセットの変更が難しい点や、サブセットのプロジェクト期間中に前工程の変更が難しいという点がデメリットとして挙げられます。

1.1.3 反復型

反復型開発は、イテレーション型開発とも呼ばれ、システム全体をいくつかの小さな機能に分割し、設計 → 実装 → テストというサイクルを、顧客が納得いく成果物ができるまで何度も繰り返す手法です。反復型開発は、イテレーティブとも呼ばれます。

反復型開発と漸進型開発は似ていますが、反復型開発では、各イテレーションで成果物の完成度を高めていくという点が異なります。

1.1.4 アジャイル型

アジャイル型開発は、要件の変更程度が高く、デリバリー頻度も高い場合に適した手法です。**短い期間（スプリント）**で開発とテストを繰り返し、顧客に価値を提供していきます。顧客とのコミュニケーションを密にとり、変化を積極的に受け入れることで、市場のニーズに迅速に対応できるというメリットがあります。

アジャイル型開発では、1週間ごとに開発チームが見積もりを行い、柔軟に計画を変更していくため、全体計画が立てづらいというデメリットがあります。また、「あれもやりたい、これもやりたい」という顧客からの要望を全て受け入れてしまうと、スケジュールや予算が膨らんでいくリスクがあります。一方で、成功率が高く、プログラマーの残業時間も少ない傾向にあります。また、他社競争力が高いというメリットもあります。

1.2 ウォーターフォール開発

ウォーターフォール開発は、従来型の開発手法であり、各工程を順番に滝が流れ落ちるように進めていくことから、その名が付けられています。各工程の成果物を明確に定義し、計画に沿って進めていくため、進捗管理が容易であり、プロジェクト全体の計画が見通しやすいため、予算やスケジュールの管理がしやすいというメリットがあります。

ウォーターフォール開発の各工程は以下の通りです。

1. 要件定義: システム開発において、顧客が求める機能や性能、制約条件などを明確にする工程です。システム開発の最初の段階で、顧客の要望をヒアリングし、実現可能な範囲でシステムの仕様を決定します。要件定義書には、機能一覧や非機能要件などが記載されます。
2. 外部設計: システム全体の設計を行い、画面設計、帳票設計、データベース設計、外部システムとの連携設計などが含まれます。外部設計では、顧客の視点でシステムの仕様を検討し、ユーザーインターフェースや操作方法などを決定します。外部設計の結果は、外部設計書としてまとめられます。
3. 内部設計: 外部設計で決定した仕様に基づき、システムの内部構造や処理ロジックなどを詳細に設計する工程です。内部設計では、プログラマーがシステムを実装するための詳細な仕様を決定します。内部設計の結果は、内部設計書としてまとめられます。
4. 実装: 内部設計で作成された設計書に基づき、プログラミング言語を用いて実際にシステムを構築する工程です。実装は、プログラマーが中心となって行います。実装の結果、プログラムコードが作成されます。
5. テスト: 開発したシステムが設計書通りに動作するか、不具合がないかを検証する工程です。テストは、単体テスト、結合テスト、総合テストの3段階に分けられます。
   • 単体テスト: 機能単位、できるだけ小さな単位でテストを行います。関数単位や画面のパーツ単位などでテストを行います。
   • 結合テスト: 複数の機能を組み合わせたテストを行い、モジュール間の連携やデータの整合性を確認します。
   • 総合テスト: システム全体を対象としたテストを行い、全ての機能が正常に動作するか、性能要件を満たしているかなどを確認します。総合テストは、システムテストやシナリオテストと呼ばれることもあります。
6. リリース: テストが完了したシステムを、実際に運用環境に導入し、利用できるようにする工程です。

ウォーターフォール開発は、各工程を順番に進めていくため、計画が立てやすく進捗管理がしやすいというメリットがあります。一方、一度開発が進んでしまうと、要件の変更に柔軟に対応することが難しく、手戻りが発生しやすいため、開発期間が長くなってしまうというデメリットもあります。ウォーターフォールモデルは、V字型開発手法と呼ばれることもあります。

ウォーターフォール開発は、要件が明確で変更が少ないシステム開発に適した手法です。しかし、近年では、システム開発のスピードアップや柔軟性の向上が求められるようになり、アジャイル開発など、より柔軟な開発手法が注目されています。

1.3 アジャイル開発

1.3.1 アジャイル開発とは

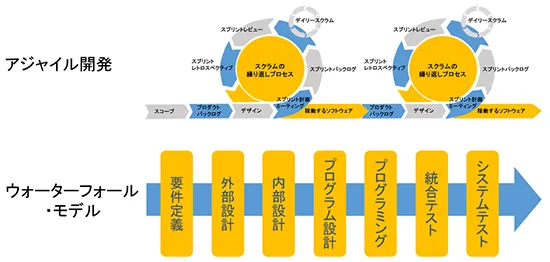
アジャイル開発とは、短いサイクルで開発とリリースを繰り返し、変化に対応する開発手法です。従来のウォーターフォール型開発とは異なり、計画に固執するのではなく、変化を積極的に受け入れることを重視します。アジャイル開発は、「ハウツー」ではなく、マインドセットや哲学であると言われています。

1.3.2 メリットとデメリット

アジャイル開発のメリットは、変更に柔軟に対応できることです。市場のニーズや顧客の要求が変化しても、迅速に対応することができます。また、短いサイクルでリリースを繰り返すため、早期に顧客に価値を提供することができます。さらに、チームメンバー間のコミュニケーションを重視するため、問題を早期に発見し、解決することができます。

一方、アジャイル開発のデメリットは、計画性が重要になることです。短いサイクルで開発を進めるため、計画がずれてしまうと、プロジェクト全体に影響が及ぶ可能性があります。また、チームメンバー全員がアジャイル開発の知識と経験を持っている必要があります。

1.3.3 適応するプロジェクト

アジャイル開発は、以下のようなプロジェクトに適しています。

• 要件が変化しやすいプロジェクト
• 競争の激しい市場
• 顧客との密な連携が必要なプロジェクト
• 早期に市場に投入する必要があるプロジェクト

1.3.4 アジャイル開発のフレームワーク - スクラム

1.3.4.1 スクラムとは

スクラムとは、アジャイル開発の代表的なフレームワークです。スクラムは、チームワークと反復的な開発を重視し、**短いサイクル（スプリント）**で開発を進めていきます。スクラムの全体像は、「3つの役割」、「5つのイベント」、「3つの作成物」で表すことができます。また、スクラムの基本は、開発者であるケン・シュエイバー氏とジェフ・サザーランド氏によって作成された「スクラムガイド」という公式ドキュメントにまとめられています。

1.3.4.2 スクラムの3つの役割

スクラムには、以下の3つの役割があります。

• プロダクトオーナー: プロダクトの価値を最大化することに責任を持ちます。プロダクトバックログの作成と管理、スプリントゴールの設定、スプリントレビューへの参加などが主な役割です。
• 開発者: プロダクトの開発を行います。スクラムでは、「開発者」はあらゆる開発作業に対応できることを前提としています。スプリントプランニングへの参加、スプリントバックログの作成、デイリースクラムへの参加などが主な役割です。
• スクラムマスター: スクラムチームがスクラムを正しく実践できるように支援します。スクラムチームと組織へのスクラム導入・定着の支援、スクラムの運用を阻害する要因を取り除く支援などが主な役割です。スクラムマスターには、サーバント・リーダーシップが求められます。

1.3.4.3 プロダクトバックログ

プロダクトバックログとは、プロジェクトの要求や顧客ニーズをリスト化したものです。プロダクトオーナーが作成し、管理します。プロダクトバックログは、常に変化するものであり、優先順位の高いものから順にスプリントバックログに反映されます。プロダクトバックログには、ユーザーストーリー形式で書かれた機能やフィーチャーのほか、バグの修正、調査、技術的負債などがタスクとして書かれることもあります。

1.3.4.4 スプリントバックログ

スプリントバックログとは、プロダクトバックログから優先度の高いものを抜粋し、計画したものです。スプリント期間中に開発者が行う作業のリストであり、開発者によって作成されます。スプリントバックログは、インクリメントをどのように生み出すかの実行可能な計画です。

1.3.4.5 ベロシティ

ベロシティとは、アジャイルチームのアウトプット能力のことです。過去の1スプリントあたりに完了したプロダクトバックログアイテムの数などを参考に算出されます。

1.3.4.6 デイリースクラム

デイリースクラムとは、毎日の開発状況の共有です。開発者は、毎日の決まった時間に集まり、昨日の進捗、今日の予定、問題点などを共有します。デイリースクラムは、課題解決を促進し、チームメンバー間のコミュニケーションを円滑にすることを目的としています。

1.3.4.7 レトロスペクティブ

レトロスペクティブとは、定期的な振り返りのことです。スプリント終了後などに、チームメンバーが集まり、スプリントを振り返り、改善点を議論します。レトロスペクティブは、チームの継続的な改善を目的としています。

2. プロジェクトマネジメントの方法

2.1 プロジェクトとは何か

2.1.1 プロジェクトの定義：独自目標と期限を持つ活動

プロジェクトとは、独自目標と期限という2つの要素を持つ活動です。言い換えれば、今までにない新しい目標を掲げ、それを期限内に達成しようとする活動がプロジェクトと言えるでしょう。

2.1.2 定常業務との違い：継続性 vs. 独自性

プロジェクトと対照的な活動として、定常業務があります。定常業務は、一般的にルーティンワークと呼ばれ、マニュアルやルールに従って、定期的に、安定的に、継続的に行われる活動です。プロジェクトが独自性の高い活動である一方、定常業務は継続性を重視する活動と言えるでしょう。

2.1.3 プロジェクトとルーティンワークの関係性

プロジェクトとルーティンワークは、ビジネスの成長において両輪のような関係にあります。まず、プロジェクト活動によって独自性の高い目標を期限内に達成することで、新しい製品、サービス、プロセスなどが生み出されます。これは、0から1を生み出す活動と言えるでしょう。次に、プロジェクトで生み出された新しいものをルーティンワーク化し、定常業務に組み込んでいきます。そして、安定的に運用することで、ビジネスはさらに成長していくのです。

2.1.4 プロジェクトマネージャーとラインマネージャーの役割分担

企業や組織内には、一般的にプロジェクトマネージャーとラインマネージャーという役割が存在します。プロジェクト活動とルーティンワークは異なる性質を持つため、それぞれを専門に担当する役割が必要となるのです。

2.2 プロジェクトマネジメントの基礎

2.2.1 プロジェクトマネジメントの定義：プロジェクトを成功に導くための活動

プロジェクトマネジメントとは、限られた資源（ヒト・モノ・カネ・情報・時間）をやりくりして、プロジェクトを成功に導くための活動です。

2.2.2 プロジェクトマネージャーの役割：目標達成のための資源配分、調整

プロジェクトマネージャーは、プロジェクトの目標達成に向けて、限られた資源を適切に配分し、関係者を調整していく役割を担います。言い換えれば、やりくりの専門家として、プロジェクトを成功へと導くことが求められます。

2.2.3 プロジェクトの立ち上げ：キックオフミーティングの重要性

プロジェクトの立ち上げにおいて、キックオフミーティングは非常に重要なイベントです。キックオフミーティングの目的は、主に2つあります。1つ目は、プロジェクトの基本情報を関係者全員で共有することです。プロジェクトの目標、スケジュール、体制、役割分担などを共有することで、共通認識を持つことができます。2つ目は、プロジェクトステークホルダー間の交流を促進することです。プロジェクトメンバー同士が互いに顔と名前を一致させ、親睦を深めることで、チームワークやコミュニケーションが向上します。

2.2.4 目標設定の重要性：目標が不明確だと、成果物や方向性がずれる

プロジェクトにおいて、目標設定は非常に重要です。目標が不明確なままプロジェクトを進めてしまうと、成果物が当初の想定と異なってしまったり、プロジェクトの方向性がずれてしまったりする可能性があります。その結果、プロジェクトが失敗に終わってしまうこともあるため、プロジェクト開始前に目標を明確化しておく必要があります。

2.3 プロジェクト計画に必要な知識

プロジェクト計画は、プロジェクトを成功に導くための羅針盤のようなものです。羅針盤なしに航海に出られないように、プロジェクト計画なしにプロジェクトをスタートさせることはできません。プロジェクト計画では、スコープ、WBS、ガントチャート、クリティカルパスといった知識が必要になります。これらの知識を身につけることで、より精度の高いプロジェクト計画を作成することができます。

2.3.1 スコープマネジメント：プロジェクトの範囲を明確化

スコープとは、日本語で「範囲」という意味です。スコープマネジメントとは、プロジェクトの範囲を明確化し、管理していくことです。プロジェクトの範囲を明確にしておくことで、後から「あれもこれもやるはずだった」といった認識の齟齬を防ぎ、プロジェクトをスムーズに進めることができます。

プロジェクト開始後にステークホルダーから様々な要求が出てくる場合がありますが、スコープマネジメントを行うことで、当初の合意事項に基づいて対応することができます。

2.3.1.1 要求事項収集：ステークホルダーのニーズを明確にする

プロジェクトの範囲を明確にするためには、まず、ステークホルダーの要求事項を収集する必要があります。要求事項とは、ステークホルダーがプロジェクトに求めるニーズのことです。インタビューやアンケート、ワークショップなどを実施することで、ステークホルダーがプロジェクトに何を求めているのかを明確にします。

ステークホルダーは、プロジェクトの影響を受ける人や組織のことで、顧客、プロジェクトメンバー、経営層、関連部署などが含まれます。それぞれのステークホルダーは、プロジェクトに対して異なる関心や立場を持っているため、それぞれのニーズを把握することが重要です。要求事項を収集する際には、ステークホルダーの立場や役割を考慮し、適切な方法で情報を収集する必要があります。

2.3.1.2 スコープ記述書：プロジェクトの範囲を文書化

収集した要求事項を基に、プロジェクトの範囲を明確に定義した文書がスコープ記述書です。スコープ記述書には、プロジェクトの目標、成果物、除外事項、制約条件などが記載されます。スコープ記述書は、プロジェクト関係者間でプロジェクトの範囲に対する共通認識を図るための重要な文書です。

スコープ記述書は、プロジェクト憲章やRFP、顧客への提案書、契約書といった情報源を基に作成されます。スコープ記述書には、プロジェクトの目的、目標、成果物、除外事項、制約条件、承認プロセス、改定履歴などが記載されます。スコープ記述書を作成することで、プロジェクト関係者間でプロジェクトの範囲に対する共通認識を持つことができ、後々のトラブルを未然に防ぐことができます。

2.3.2 WBS（作業分解構成図）：成果物と作業を階層的に分解

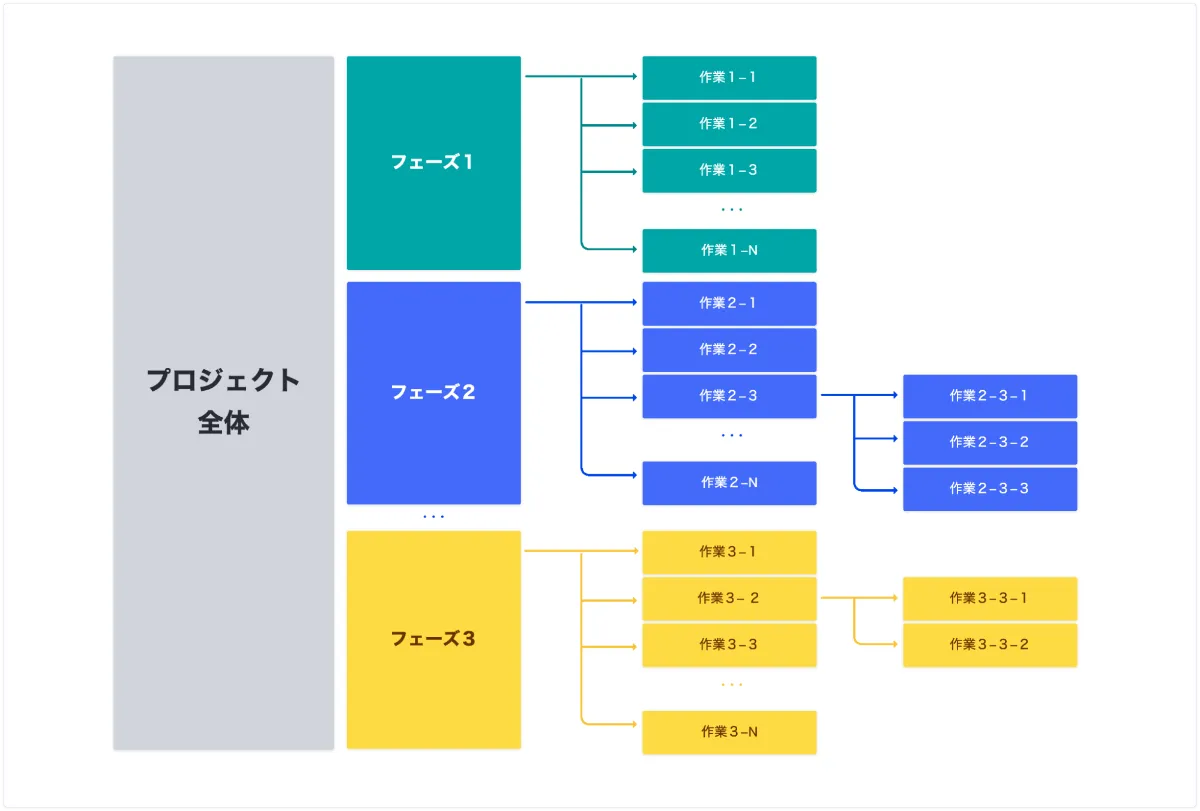
WBS（Work Breakdown Structure）は、プロジェクトの成果物と作業を階層的に分解した図です。プロジェクトの目標を達成するために、どのような成果物が必要で、そのためにはどのような作業が必要なのかを、ツリー構造で表現します。WBSは、プロジェクト計画の基礎となる重要なツールです。

WBSは、プロジェクト名や最終成果物を最上位レベル（レベル1）に置き、そこから成果物、要素成果物、活動と階層を下げて詳細化していきます。例えば、ペットボトル飲料の製品開発プロジェクトの場合、レベル1は「お茶新製品プロジェクト」、レベル2は「キャップ」「ボトル」「ラベル」「内容液」といった成果物、レベル3は「キャップの設計」「ボトルの製造」「ラベルのデザイン」「内容液の配合」といった要素成果物、レベル4は「キャップの設計図作成」「ボトルの金型製作」「ラベルの印刷業者選定」「内容液の試作品作成」といった活動になります。WBSを作成することで、プロジェクト全体の作業を把握しやすくなり、作業の抜け漏れを防ぐことができます。また、WBSは、スケジュール管理やコスト管理の基礎となる重要な資料となります。

WBSの作成方法には、成果物で分解する方法とプロセスで分解する方法があります。成果物で分解する場合は、最終成果物を構成する要素成果物に分解し、さらに要素成果物を構成する活動に分解していきます。プロセスで分解する場合は、プロジェクトの開始から終了までのプロセスをいくつかの段階に分け、それぞれの段階に必要な作業を分解していきます。

WBSを作成する際の注意点としては、成果物の粒度を揃えること、作業の重複を防ぐこと、担当者や期間を明確にすることなどが挙げられます。

2.3.3 ガントチャート：タスクの開始・終了時期、担当者、進捗を可視化

ガントチャートは、プロジェクトのタスクの開始・終了時期、担当者、進捗状況を可視化した図です。横軸に時間、縦軸にタスクを配置し、各タスクの期間を棒グラフで表します。ガントチャートは、プロジェクトのスケジュール管理に役立つツールです。

ガントチャートを作成する際には、WBSで洗い出したタスクを基に、各タスクの開始・終了時期、担当者、所要期間などを設定します。ガントチャートは、プロジェクトの進捗状況を把握し、遅延が発生している場合は対策を講じるために利用されます。

ガントチャートを作成する際の注意点としては、タスクの依存関係を明確にすること、バッファを設定すること、定期的に更新することなどが挙げられます。タスクの依存関係とは、あるタスクが完了しないと次のタスクを開始できないという関係のことです。バッファとは、タスクの遅延に備えて余裕を持たせた期間のことです。

2.3.4 クリティカルパス：プロジェクト全体の期間に影響を与える経路

クリティカルパスとは、プロジェクト全体の期間に影響を与えるタスクの連なりのことです。複数のタスクが並行して進むプロジェクトにおいて、最も長い期間を要する経路がクリティカルパスとなります。クリティカルパスは、プロジェクト全体の期間を決定する重要な要素です。

クリティカルパス上のタスクが遅延すると、プロジェクト全体の期間も遅延してしまうため、プロジェクトマネージャーはクリティカルパスを把握し、重点的に管理する必要があります。クリティカルパスを把握することで、プロジェクトの短縮にも役立ちます。クリティカルパス上のタスクを短縮することで、プロジェクト全体の期間を短縮することができます。

クリティカルパスを管理する際の注意点としては、クリティカルパス上のタスクの進捗状況を常に監視すること、クリティカルパス上のタスクに遅延が発生した場合は、速やかに対策を講じることが挙げられます。

2.4 リスクマネジメント

プロジェクトを進める上で、リスクは避けて通れません。リスクマネジメントとは、プロジェクトに潜むリスクを特定し、分析し、対応することで、プロジェクトへの影響を最小限に抑えるためのプロセスです。リスクマネジメントは、プロジェクトの成功確率を高める上で非常に重要な要素です。

2.4.1 リスク管理と課題管理の違い：発生前と発生後

リスク管理と課題管理は、どちらもプロジェクトをスムーズに進める上で重要なプロセスですが、その対象が異なります。

リスク管理は、将来発生する可能性のある問題や不確実性に対して、事前に対策を講じるプロセスです。課題管理は、すでに発生している問題に対して、解決策を講じるプロセスです。

2.4.2 リスクの種類：好機のリスクと脅威のリスク

リスクには、プロジェクトにプラスの影響を与える「好機のリスク」と、マイナスの影響を与える「脅威のリスク」の2種類があります。

• 好機のリスク: 設定した基準よりも良い結果をもたらす可能性のことです。
• 脅威のリスク: 設定した基準よりも悪い結果をもたらす可能性のことです。

日本では、脅威のリスク、つまりプロジェクトに悪影響を与える可能性に焦点を当ててリスク管理を行うことが多いですが、好機のリスクを積極的に捉え、プロジェクトをより良い方向に進めることも重要です。

2.4.3 リスクマネジメントの進め方：リスク特定→定性分析→定量分析→対策

リスクマネジメントは、一般的に以下の4つのステップで進められます。

1. リスク特定: プロジェクトに潜むリスクを洗い出す
2. 定性リスク分析: リスクの発生確率と影響度を評価し、優先順位をつける
3. 定量リスク分析: リスクの影響度を数値化し、対策の費用対効果を分析
4. リスク対応: リスクへの対策を実施する

2.4.4 リスク登録簿：リスクを一覧化し、管理

リスク登録簿は、特定されたリスクを一覧化し、管理するための文書です。リスク登録簿には、リスクの内容、発生確率、影響度、対策、担当者などの情報が記載されます。リスク登録簿は、リスクの特定、分析、対応、監視といったリスクマネジメントのプロセス全体を通じて活用されます。

2.4.5 定性リスク分析：リスクの発生確率と影響度を評価

定性リスク分析では、特定されたリスクの発生確率と影響度を評価し、優先順位をつけます。リスクの発生確率と影響度は、過去の経験や専門家の意見などを参考に判断します。定性分析では、数値化できない要素を分析します。リスクは目に見えないため、最初から数値で表現することは難しいです。優先順位をつけることで、限られたリソースを効果的に活用し、重要なリスクから対策することができます。

2.4.6 定量リスク分析：リスクを数値化し、対策の費用対効果を分析

定量リスク分析では、定性リスク分析で評価したリスクの影響度を数値化し、対策の費用対効果を分析します。リスクの影響度を数値化することで、リスクがプロジェクトに与える影響をより具体的に把握することができます。対策の費用対効果を分析することで、どの対策が最も効果的であるかを判断することができます。

2.4.7 リスク対応：回避、軽減、転嫁、受容

リスク対応には、以下の4つの方法があります。

• 回避: リスクの発生源を取り除くことで、リスクを完全に回避する方法です。
• 軽減: リスクの発生確率や影響度を低下させる方法です。
• 転嫁: リスクを他の組織や個人に転嫁する方法です。例えば、保険に加入するなどが挙げられます。
• 受容: リスクを受け入れる方法です。リスクの発生確率や影響度が低い場合などに選択されます。

どの方法を選択するかは、リスクの性質やプロジェクトの状況などを考慮して判断します。

2.5 ステークホルダーマネジメント

プロジェクトを成功させるためには、プロジェクトに関わる様々な人たちとの良好な関係を築くことが重要です。ステークホルダーマネジメントは、プロジェクトに関わる人たちのニーズや期待を理解し、適切なコミュニケーションと対応を行うことで、プロジェクトの円滑な推進と成功を支援するプロセスです。

2.5.1 ステークホルダーとは:プロジェクトに利害関係を持つ個人や組織

ステークホルダーとは、プロジェクトに利害関係を持つ個人や組織のことです。プロジェクトの成功によって利益を得たり、逆に失敗によって損害を被ったりする可能性があります。ステークホルダーには、以下のような人たちが含まれます。

• プロジェクトオーナー
• プロジェクトチームメンバー
• 顧客
• サプライヤー
• 経営層
• 社内の関係部署
• 地域住民

2.5.2 ステークホルダー特定：プロジェクトに関係する人を洗い出す

ステークホルダーマネジメントの最初のステップは、プロジェクトに関わるステークホルダーを特定することです。プロジェクト憲章や要件定義書、RFP、提案書、契約書などの資料を参考にしたり、関係者にインタビューを行ったりすることで、ステークホルダーを洗い出します。

2.5.3 ステークホルダー分析：影響力、関心度、賛否などを分析

ステークホルダーを特定したら、次にそれぞれのステークホルダーの影響力、関心度、プロジェクトへの賛否などを分析します。

ステークホルダーの影響力と関心度を分析する際には、以下のような2軸のマトリックスを用いることが一般的です。

• 縦軸：プロジェクトへの権限
• 横軸：プロジェクトへの興味関心

このマトリックス上に、特定したステークホルダーをプロットすることで、どのステークホルダーを重点的に管理するべきかを判断することができます。例えば、プロジェクトへの権限が高く、興味関心も高いステークホルダーは、プロジェクトに大きな影響を与える可能性があるため、特に注意深くコミュニケーションをとる必要があります。

2.5.4 ステークホルダー管理表：ステークホルダー情報を一元管理

ステークホルダー管理表は、ステークホルダーに関する情報を一元管理するための表です。ステークホルダー管理表には、以下のような項目を記載します。

• 氏名
• 所属組織
• 役職
• 連絡先
• 関心事項
• 影響力
• 賛否
• 対応方針
• 対応内容
• 期待される成果
• 情報共有方法
• コミュニケーション頻度

ステークホルダー管理表を作成することで、ステークホルダーに関する情報を整理し、共有することができます。また、ステークホルダーへの対応状況を記録することで、適切なコミュニケーションを継続的に行うことができます。ステークホルダーの状況や状態は時間とともに変化するため、ステークホルダー管理表も定期的に更新することが重要です。

ステークホルダーマネジメントは、プロジェクトの成功に不可欠な要素です。ステークホルダーとの良好な関係を築くことで、プロジェクトを円滑に進め、成功に導くことができます。

2.6 チームマネジメント

プロジェクトの成功は、チームメンバーの能力と連携にかかっています。チームマネジメントは、個々の能力を最大限に引き出し、チームとして最大の成果を出すために非常に重要です。

2.6.1 チームの生産性を考慮したスケジュール管理

プロジェクトのスケジュールは、チーム全体の生産性を最大化するように綿密に計画する必要があります。各メンバーのスキル、経験、作業量を考慮し、無理のない現実的なスケジュールを作成することが重要です。

2.6.2 スケジュールバッファ：不確実性に対応するための時間的余裕

プロジェクトには、予期せぬ問題や遅延が発生することがあります。スケジュールバッファは、こうした不確実性に対応するために、スケジュールに余裕を持たせることを意味します。個々のタスクレベルではなく、プロジェクト全体でバッファを管理する方が効果的です。

2.6.3 チーム憲章：チームの行動規範、コミュニケーションルールなどを明文化

チーム憲章は、チームメンバーが共有すべき行動規範やコミュニケーションルールなどを明確にした文書です。チーム憲章を作成することで、チームメンバーの共通認識を形成し、チームとしての結束力を高めることができます。

明確にすべき項目の例:

• チームの価値観: 会社のミッション、ビジョン、バリューに沿ったもの
• コミュニケーションガイドライン: 会議の方法、報告の頻度、連絡手段など
• 意思決定の基準とプロセス: どの程度の権限で誰が決定するか
• コンフリクトの解決プロセス: 意見の相違があった場合の対処法
• 会議のガイドライン: 時間厳守、目的の共有、議題設定など
• チーム合意事項: その他、チームとして守るべきこと

2.6.4 モチベーションマネジメント：持続的なモチベーション向上施策の重要性

チームメンバーのモチベーションは、プロジェクトの成果に大きく影響します。チームメンバーが常に高いモチベーションを維持できるよう、以下の様な施策を継続的に実施していくことが重要です。

• チームメンバーの意見を尊重する
• 成果を適切に評価し、フィードバックする
• チームで目標を共有し、達成感を共有する
• スキルアップの機会を提供する
• 快適な労働環境を提供する

モチベーションマネジメントは、短期的な視点ではなく、長期的な視点に立って取り組むことが重要です。

2.7 リーダーシップ：プロジェクト成功の鍵

プロジェクトを成功に導く上で、リーダーシップは欠かせません。リーダーシップを効果的に発揮することで、チームメンバーを一つにまとめ、共通の目標達成へと導くことができます。

2.7.1 サーバントリーダーシップ：メンバーを支え、成長を促すリーダーシップ

サーバントリーダーシップとは、メンバーを支援し、成長を促すことに重きを置くリーダーシップスタイルです。従来型のリーダーシップのように、上司として支持や命令によってメンバーを従わせるのではなく、メンバー一人ひとりの自主性を尊重し、能力を最大限に引き出すことで、チームとしての成果を最大化することを目指します。

PMP試験対策として、サーバントリーダーシップのイメージを掴んでおくことは非常に重要です。PMI（Project Management Institute）は、サーバントリーダーシップをプロジェクトマネジメントにおいて重要な要素として位置づけています。そのため、PMP試験問題においても、サーバントリーダーの行動として適切かどうかを問われる可能性があります。

サーバントリーダーシップは、1970年代に提唱され、近年、その重要性が再認識されています。現代社会は、テクノロジーの進化が速く、社会環境の変化も激しい時代です。このような時代においては、トップダウン型のリーダーシップでは、変化への対応が遅れてしまう可能性があります。そこで、メンバーの自主性を重んじ、変化に柔軟かつ迅速に対応できるサーバントリーダーシップが求められているのです。

サーバントリーダーには、以下のような10個の特性があるとされています。

• 傾聴力：メンバーの意見に真摯に耳を傾け、共感する
• 共感力：メンバーの気持ちを理解し、寄り添う
• 癒やしの力：メンバーの心の傷を癒し、サポートする
• 自己認識：自分の強みや弱みを理解し、行動に活かす
• 説得力：論理的な思考に基づき、メンバーを納得させる
• 概念化：目標を明確化し、メンバーに共有する
• 先見力：過去の経験や教訓を活かし、未来を予測する
• 執事役：メンバーの成長を支援し、利益を与える
• 人々への成長の関与：メンバーの能力や可能性を信じ、成長を支援する
• コミュニティづくり：メンバーが安心して成長できる環境を作る

これらの特性を持つサーバントリーダーは、チームメンバーから支持され、厚い信頼を得ることができます。

2.7.2 SL理論：状況に応じた4つのリーダーシップスタイルを使い分ける

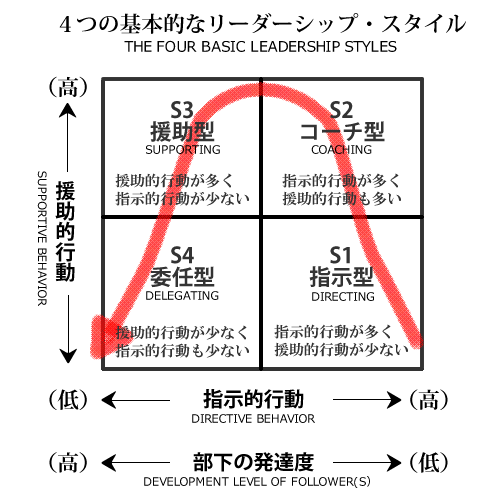
SL理論（Situational Leadership Theory）とは、リーダーが置かれた状況に応じて適切なリーダーシップスタイルを使い分けることで、チームの成果を最大化できるという考え方です。SL理論では、以下の2つの軸で状況を分析します。

• コンピテンス（能力）：依頼するタスクに対するメンバーのスキルや経験
• コミットメント（意欲）：依頼するタスクに対するメンバーの意欲や積極性

そして、これらの軸に基づき、4つのリーダーシップスタイルを使い分けます。

• 指示型：メンバーのコンピテンスが低く、コミットメントも低い場合は、リーダーが具体的な指示を与え、進捗を細かく管理する
• コーチング型：メンバーのコンピテンスは低いが、コミットメントは高い場合は、リーダーが指導や助言を行いながら、メンバーの成長を促す
• 支援型：メンバーのコンピテンスは高いが、コミットメントが低い場合は、リーダーがメンバーの意見を尊重し、モチベーションを高めるような働きかけをする
• 委任型：メンバーのコンピテンスもコミットメントも高い場合は、リーダーは目標設定と進捗確認のみを行い、メンバーに自主性を委ねる

SL理論は、あらゆる状況において、万能なリーダーシップスタイルは存在しないという考え方に基づいています。リーダーは、常にメンバーの状況を把握し、適切なリーダーシップスタイルを選択することで、チームを成功に導くことができます。

SL理論を実践する上での重要なポイントは以下の2点です。

1. リーダーシップスタイルの切り替えは段階的に行う
2. タスクの難易度によってもリーダーシップスタイルは変化する

リーダーは、メンバーの状況やタスクの難易度を考慮しながら、SL理論を柔軟に活用することで、チーム全体の能力を高め、プロジェクトの成功確率を高めることができます。

2. プロジェクトマネジメントの方法とその重要性

ここまでの章では、システム開発の手法であるアジャイル開発とウォーターフォール開発、そしてプロジェクトを成功させるためのプロジェクトマネジメントについて解説しました。

システム開発において、ウォーターフォール開発は各段階を順次進める伝統的な手法ですが、変化への対応が難しいという側面があります。一方、アジャイル開発は短いサイクルで開発とフィードバックを繰り返すことで、柔軟な対応を可能にします。どちらの手法が適しているかは、プロジェクトの特性や顧客のニーズによって異なります。

プロジェクトマネジメントは、限られたリソースの中で目標達成を目指すための重要なプロセスです。スコープ、スケジュール、コスト、リスク、コミュニケーション、ステークホルダーといった様々な要素を適切に管理することで、プロジェクトの成功確率を高めることができます。

プロジェクトを成功させるためには、チームマネジメントも重要です。メンバーのモチベーションを高め、個々の能力を最大限に引き出すためには、生理的衝動要因、外的要因、内的要因といったモチベーションの要素を理解し、ハーズバーグの二要因理論に基づいた適切なマネジメントを行う必要があります。

さらに、プロジェクトマネージャーには、チームを導くための適切なリーダーシップが求められます。メンバーを支援し成長を促すサーバントリーダーシップや、状況に応じて適切なスタイルを使い分けるSL理論など、様々なリーダーシップ理論を理解し、実践することが重要です。

これらの要素を総合的に理解し、状況に合わせて適切な方法を選択・実行することで、プロジェクトを成功に導くことができます。次の章では、プロジェクトマネジメントの手法を支える理論的な基盤として、グラフ理論の基本概念とその応用について解説します。グラフ理論は、プロジェクトの複雑な要素間の関係を視覚化し、分析するための強力なツールです。これにより、プロジェクトの計画や管理において、より効果的な意思決定が可能となります。

Ⅰ. グラフ理論入門

この章では、マッチング問題を理解する上で必要なグラフ理論の基礎知識を解説していきます。

1. グラフの基礎

まず、グラフとは何か、そしてグラフの基本的な用語について説明します。

1.1 グラフの定義と種類

グラフとは、頂点と呼ばれる点と、頂点同士を結ぶ辺と呼ばれる線で構成される図形のことです。

グラフは、多重グラフと単純グラフ、無向グラフと有向グラフなどに分類できます。

• 多重グラフ：2つの頂点間に複数の辺が存在したり、1つの頂点から出て自身に戻る辺（自己ループ）を持つグラフのことです。現実世界では、例えば、都市間を結ぶ複数の道路がある場合など、多重グラフで表現すると便利な場合があります。
• 単純グラフ：多重辺や自己ループを含まないグラフのことです。本記事では、特に断りがない限り、単純グラフを扱います。
• 無向グラフ：辺に向きがないグラフのことです。
• 有向グラフ：辺に向きがあるグラフのことです。辺に向きがあるということは、一方通行の道路のような関係を表す際に便利です。有向グラフの辺は特にアークと呼ぶこともあります。

1.2 頂点、辺、次数、隣接

• 頂点 (vertex)：グラフを構成する点のことです。
• 辺 (edge)：グラフを構成する、頂点同士を結ぶ線のことです。
• 次数 (degree)：グラフの各頂点から出ている辺の数のことです。次数が偶数の頂点を 偶点、奇数の頂点を 奇点 と呼びます。
• 隣接 (adjacent)：2つの頂点が辺で直接結ばれているとき、それらの頂点は隣接していると言います。

例えば、友達関係を表すグラフを考えましょう。このグラフの頂点は人を表し、辺は友達関係を表すとします。

• 頂点Aの次数が3であるということは、Aさんに友達が3人いることを意味します。
• 頂点BとCが辺で結ばれているということは、BさんとCさんが友達であることを意味します。

1.3 パス、サイクル、連結性

グラフ上の頂点を辿る経路について、いくつかの重要な概念を紹介します。

• 歩道 (walk)：グラフ中の頂点と辺を交互に並べた列のことです。同じ頂点や辺を何度通っても構いません。
• 小道 (trail)：辺を重複して通らない歩道のことを小道と言います。
• 回路 (circuit) / 閉じた小道：始点と終点が一致する小道のことを回路または閉じた小道と言います。
• パス (path)：頂点も辺も重複して通らない歩道のことをパスと言います。
• 閉路 / サイクル (cycle)：始点と終点が一致するパスのことを閉路またはサイクルと言います。

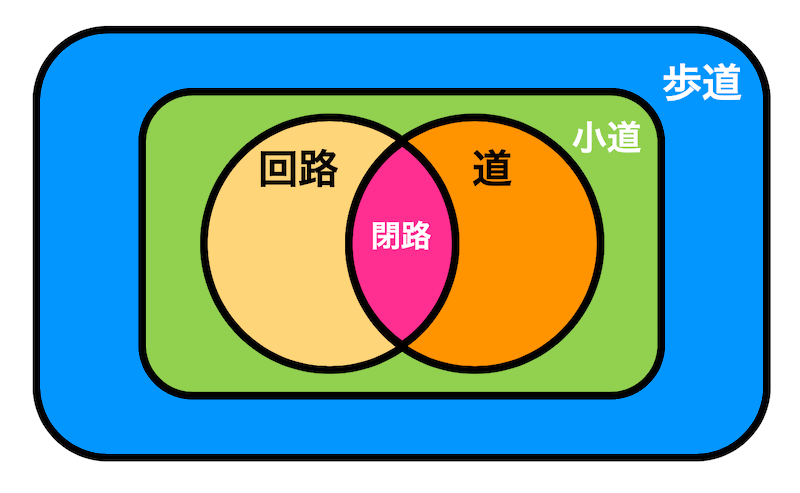
これらの概念は、例えば、ある地点から別の地点への経路を考える際に重要となります。

• 歩道は、出発地から目的地までの経路を、寄り道や同じ道を何度も通ることを許して表したものと言えます。
• パスは、同じ場所を二度と通らない最短経路を表す際に使われます。

これらの概念を理解しておくことは、グラフ理論を学ぶ上で非常に重要です。

1.4 木、森とその性質

• 木 (tree)：閉路を持たない連結グラフのことです。木は、階層構造を持つデータ構造を表す際にしばしば用いられます。
• 森 (forest)：閉路を含まず、連結とは限らないグラフのことです。森は、複数の木が集まったものと考えることができます。

木については、以下の重要な性質が成り立ちます。

• 木は連結で、かつ、辺を一つ削除すると必ず非連結になる。：木は、連結性を保つために必要最低限の辺の数しか持たないグラフであると言えます。
• 木の辺の数は、頂点の数より1つ少ない。：これは、木構造の基本的な性質の一つであり、様々な場面で応用されます。

これらの性質は、木構造を扱うアルゴリズムを設計する上で重要な役割を果たします。

2. グラフの探索アルゴリズム

この章では、グラフ上の頂点を効率的に探索するアルゴリズムである、幅優先探索 (BFS) と 深さ優先探索 (DFS) について解説します。これらのアルゴリズムは、グラフ理論における多くの問題を解くための基礎となります。

2.1 幅優先探索 (BFS) とその応用

幅優先探索 (Breadth-First Search, BFS) は、グラフの始点から近い頂点を優先的に探索していくアルゴリズムです。具体的には、始点から距離1の頂点を全て訪問し、次に距離2の頂点を全て訪問し、というように、距離の順に探索を進めていきます。

BFSは、以下のような手順で実行されます。

1. 始点を訪問済みにし、キューに追加します。
2. キューが空になるまで、以下の処理を繰り返します。
   • キューから先頭の頂点を取り出します。
   • 取り出した頂点に隣接する未訪問の頂点を全て訪問済みにし、キューに追加します。

BFSは、迷路の最短経路を求める問題など、様々な問題に応用できます。例えば、迷路のスタート地点からゴール地点までの最短経路を求める場合、BFSを用いることで、スタート地点から近い順にマス目を探索していくため、最短経路でゴールにたどり着くことができます。

2.2 深さ優先探索 (DFS) とその応用

深さ優先探索 (Depth-First Search, DFS) は、グラフの始点から可能な限り深く探索を進めていくアルゴリズムです。具体的には、始点から出発し、隣接する未訪問の頂点があれば、その頂点を訪問し、さらにその頂点から隣接する未訪問の頂点があれば訪問し、というように、可能な限り深くまで探索を進めます。行き止まりに達したら、一つ前の頂点に戻り、そこから別の経路を探索します。

DFSは、以下のような手順で実行されます。

1. 始点を訪問済みにします。
2. 訪問した頂点に隣接する未訪問の頂点があれば、その頂点を訪問し、この手順を再帰的に繰り返します。
3. 隣接する未訪問の頂点がなくなったら、一つ前の頂点に戻ります。

DFSは、グラフの構造を調べる問題など、様々な問題に応用できます。例えば、グラフが連結かどうかを判定する問題や、グラフに閉路が含まれているかどうかを判定する問題などを、DFSを用いて効率的に解くことができます。

これらの探索アルゴリズムは、グラフ理論における基礎的なアルゴリズムであり、様々な問題に応用されています。

3. オイラーグラフとハミルトングラフ

この章では、特別な性質を持つグラフであるオイラーグラフとハミルトングラフについて解説します。これらのグラフは、それぞれ「一筆書き問題」と「巡回セールスマン問題」と呼ばれる古典的な問題と密接に関係しており、現実世界にも多くの応用例があります。

3. オイラーグラフとオイラー回路：一筆書き問題

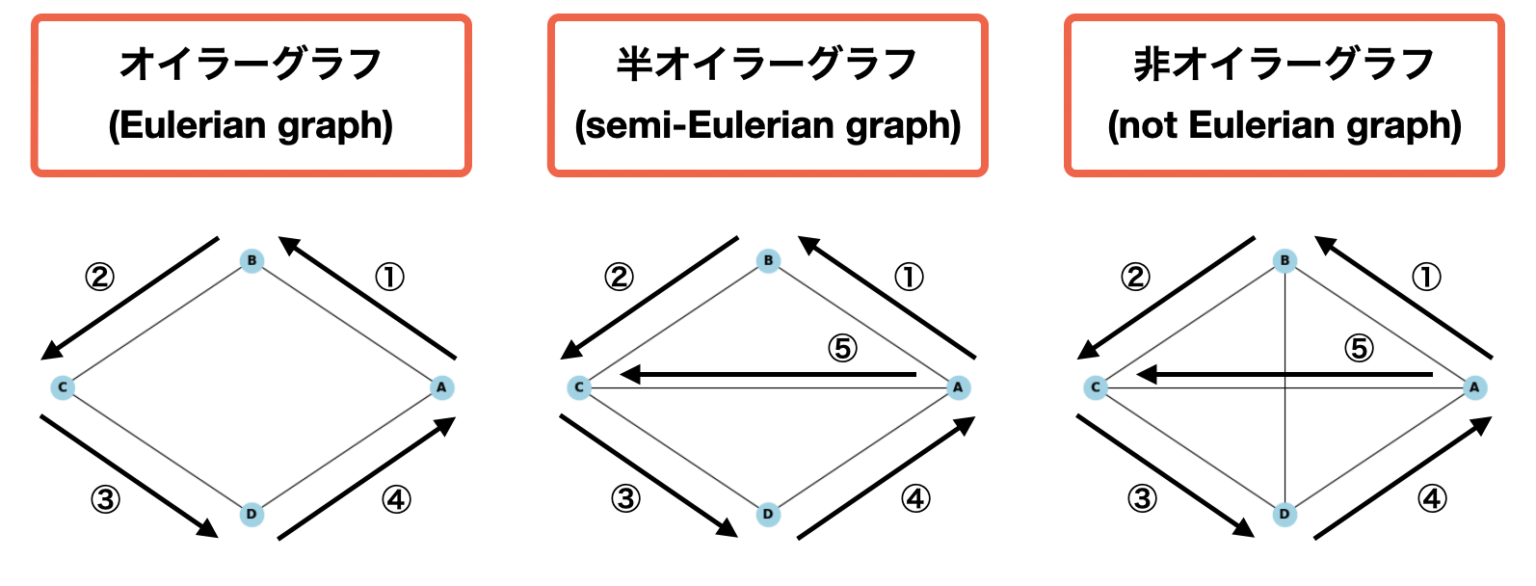
3.1 オイラーグラフとオイラー回路の定義

オイラーグラフとは、グラフのすべての辺をちょうど一回だけ通るような閉じた経路が存在するグラフのことです。このような経路をオイラー回路と呼びます。

オイラーグラフの例として、有名な「ケーニヒスベルクの橋の問題」があります。この問題は、7つの橋を持つケーニヒスベルクの街において、すべての橋をちょうど一回だけ渡って元の場所に戻ってくることができるか、という問題です。オイラーは、この問題をグラフ理論を用いて解決し、オイラーグラフとオイラー回路の概念を確立しました。

3.2 オイラーグラフの判定方法

グラフがオイラーグラフであるかどうかは、以下のシンプルな条件で判定できます。

定理：連結なグラフがオイラーグラフであるための必要十分条件は、すべての頂点の次数が偶数であることである。

この定理を用いることで、与えられたグラフがオイラーグラフであるかどうかを容易に判定することができます。

3.3 オイラー回路を求めるアルゴリズム：フラーリのアルゴリズム

オイラーグラフにオイラー回路が存在することがわかったら、次は実際にオイラー回路を求める方法を探求しましょう。オイラー回路を求めるアルゴリズムの一つに、フラーリのアルゴリズムがあります。

フラーリのアルゴリズムは、以下の手順でオイラー回路を求めます。

1. グラフの任意の頂点から出発する。
2. 以下のルールに従って、まだ通っていない辺を辿っていく。
   • 可能な限り、橋となる辺を辿らない。ただし、橋しか選択肢がない場合は、橋を辿る。
   • 孤立点が生じたら、その孤立点を除去する。
3. すべての辺を辿ったら、アルゴリズムは終了する。

フラーリのアルゴリズムに従って辺を辿っていくと、最終的にオイラー回路が得られます。

4. ハミルトングラフとハミルトン閉路：巡回セールスマン問題

4.1 ハミルトングラフとハミルトン閉路の定義

ハミルトングラフとは、グラフのすべての頂点をちょうど一回だけ通る閉じた経路が存在するグラフのことです。このような経路をハミルトン閉路と呼びます。

ハミルトングラフの例として、有名な「巡回セールスマン問題」があります。この問題は、複数の都市と都市間の移動距離が与えられたとき、すべての都市をちょうど一回だけ訪問して出発都市に戻る最短経路を求める問題です。この問題は、グラフ理論では、与えられたグラフにハミルトン閉路が存在するかどうかを判定し、存在する場合はその閉路を求める問題として定式化されます。

4.2 ハミルトングラフの判定方法

オイラーグラフとは異なり、ハミルトングラフであるかどうかを判定する簡単な必要十分条件は存在しません。ただし、ハミルトングラフであるための十分条件や必要条件はいくつか知られており、これらの条件を用いることで、グラフがハミルトングラフであるかどうかをある程度絞り込むことができます。

4.3 ハミルトン閉路を求めるアルゴリズム

ハミルトン閉路を求める効率的なアルゴリズムは、一般的には存在しません。これは、ハミルトン閉路問題はNP困難と呼ばれる問題のクラスに属しており、多項式時間で解くことが難しいとされているためです。

4.4 それぞれの応用例とアルゴリズム

オイラーグラフとハミルトングラフは、どちらも現実世界における様々な問題に応用されています。

4.4.1 オイラーグラフの応用例

• 道路網の設計: 道路の清掃や点検など、すべての道路を無駄なく巡回する必要がある場合に、オイラーグラフの概念が役立ちます。

5. 平面グラフと彩色問題

この章では、平面上に辺が交差することなく描画できるグラフ、平面グラフについて解説し、関連するオイラーの公式やグラフの彩色問題における4色定理、5色定理について説明します。

5.1 平面グラフと平面描画

平面グラフとは、辺が交差することなく平面上に描画できるグラフのことです。このようなグラフの描画を平面描画と呼びます。平面グラフは、地図の領域分割、回路設計、化学構造式など、様々な場面で現れる重要な概念です。

例えば、地図上にいくつかの国が描かれており、隣接する国々を線で結んだとします。このとき、線が交差しないように地図を描くことができれば、その地図は平面グラフとして表現できます。

5.2 オイラーの公式とその応用

平面グラフに関して重要な定理の一つに、オイラーの公式があります。この公式は、連結な平面グラフの頂点の数 (v)、辺の数 (e)、面の数 (f) の間に成り立つ以下の関係式を示しています。

v - e + f = 2

オイラーの公式は、平面グラフの性質を調べる上で非常に有用なツールであり、様々な応用があります。例えば、この公式を用いると、平面グラフの最大の辺数は 3v - 6 であることを証明できます。

5.3 グラフの彩色問題：4色定理、5色定理

グラフの彩色問題とは、グラフの隣接する頂点が異なる色で塗られるように、頂点に色を割り当てる問題です。特に、平面グラフの彩色問題は、地図の彩色問題と密接に関係しており、歴史的に見ても多くの関心を集めてきました。

5.3.1 4色定理

4色定理は、「任意の平面グラフは4色で彩色可能である」という定理です。この定理は、19世紀半ばに提唱されて以来、長い間未解決問題でしたが、1976年にAppelとHakenによってコンピュータを用いた証明が発表されました。4色定理は、地図の彩色問題において、どんな複雑な地図でも4色あれば塗り分けられることを保証するものであり、その応用範囲は多岐にわたります。

5.3.2 5色定理

5色定理は、「任意の平面グラフは5色で彩色可能である」という定理です。4色定理と比べると弱い主張にはなりますが、5色定理の証明は4色定理よりもシンプルであり、人間の手によって証明することができます。5色定理の証明は、グラフの次数に関する議論と数学的帰納法を用いることで行われます。

まとめ

平面グラフと彩色問題は、グラフ理論において重要なテーマです。オイラーの公式は平面グラフの性質を理解する上で強力なツールであり、4色定理、5色定理はグラフの彩色問題における金字塔です。これらの概念は、地図の彩色問題以外にも、回路設計、コンピュータグラフィックス、地理情報システムなど、幅広い分野で応用されています。

II. マッチング問題詳解

1. マッチング問題とは

1.1 マッチングの定義と種類

マッチング問題とは、グラフ理論において、グラフの頂点集合を2つの互いに素な集合に分割し、異なる集合に属する頂点間を辺で結ぶ問題です。具体的には、2つの集合を「男性」と「女性」と見立て、互いに好意を持つペアを辺で結んだグラフを考えます。このとき、マッチングとは、どの2つの辺も端点を共有しない、つまり一人の人が同時に2人以上とペアにならないような辺の集合を指します。

マッチングには、いくつかの種類があります。

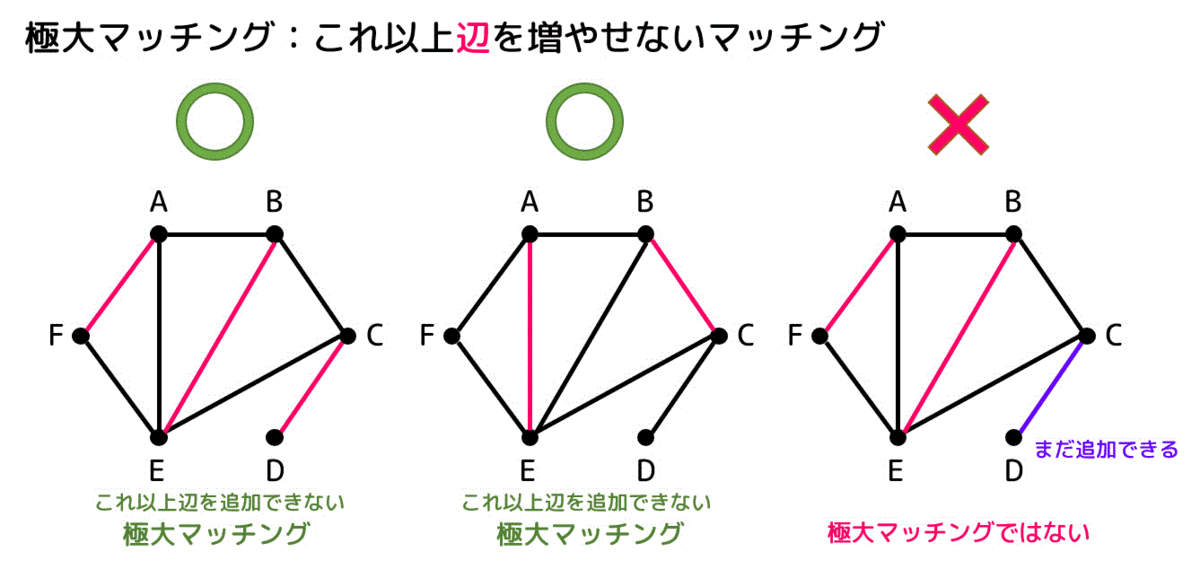
• 極大マッチング: マッチングに含まれない辺を新たに加えることができなくなった状態のマッチング。
• 最大マッチング: マッチングに含まれる辺の数が最大となっているマッチング。
• 完全マッチング: 全ての頂点がマッチングされている状態のマッチング。

1.2 実社会におけるマッチングの例

マッチング問題は、現実世界において様々な場面で現れます。以下に、具体的な例を挙げます。

• 臨床研修病院割当: 日本やアメリカでは、医学部を卒業した研修医を病院に割り当てる際に、マッチング理論が応用されています。研修医と病院はそれぞれ希望する相手を順位付けし、アルゴリズムによって最適なマッチングが決定されます。
• 仕事割り当て: 企業が求職者を採用する際にも、マッチング問題として捉えることができます。企業は求める人物像、求職者は希望する仕事内容や条件を提示し、互いに合意できるマッチングを探します。
• プレゼント: 複数の人にプレゼントを贈る際、それぞれの人が喜ぶプレゼントを1つずつ渡したい場合、マッチング問題として考えることができます。
• 結婚: 結婚相談所などでは、登録者間の相性や希望条件を考慮して、最適な結婚相手をマッチングする際に、マッチング理論が活用されています。

これらの例からわかるように、マッチング問題は、限られた資源や機会を効率的かつ公平に分配する必要がある様々な場面で応用されています。

2. 二部グラフにおけるマッチング

この章では、二部グラフにおけるマッチングについて詳しく解説していきます。二部グラフは、マッチング問題を扱う上で基礎となる重要なグラフ構造であり、現実世界の問題をモデル化する際にも頻繁に登場します。

2.1 二部グラフとマッチング

2.1.1 二部グラフの定義

二部グラフとは、頂点集合を2つの互いに素な集合（例えば、男性の集合と女性の集合）に分割し、異なる集合に属する頂点間のみを辺で結ぶことができるグラフです。つまり、同じ集合に属する頂点同士を結ぶ辺は存在しません。

2.1.2 二部グラフにおけるマッチング

二部グラフにおけるマッチングとは、どの2つの辺も端点を共有しない辺の集合のことです。言い換えれば、マッチングに含まれる辺は、互いに独立していて、共通の頂点を持たないということです。

2.2 完全マッチングと最大マッチング

2.2.1 完全マッチング

完全マッチングとは、二部グラフの全ての頂点が、マッチングに含まれる辺のいずれかの端点となっている状態を指します。つまり、全ての頂点が、ちょうど1つの辺によってペアになっている状態です。

2.2.2 最大マッチング

最大マッチングとは、マッチングに含まれる辺の数が最大となっているマッチングのことです。最大マッチングは、必ずしも完全マッチングであるとは限りません。なぜなら、二部グラフの一方の集合の要素数が、もう一方の集合の要素数よりも少ない場合、完全マッチングは存在し得ないからです。

2.3 ホールの結婚定理

ホールの結婚定理は、二部グラフにおいて完全マッチングが存在するための必要十分条件を与える重要な定理です。この定理は、結婚問題として表現されることが多く、以下のように述べられます。

ホールの結婚定理: n人の女性と男性がいて、各女性はm人の男性と知り合いであるとする（mは任意の自然数）。このとき、全ての女性が異なる男性と結婚できるための必要十分条件は、以下の条件を満たすことである。

• 任意のk人の女性（1 ≤ k ≤ n）は、合わせて少なくともk人の男性と知り合いである。

この定理は、一見すると自明のように思えるかもしれませんが、マッチング問題の理論的な基礎を築く上で重要な役割を果たしています。

例: 3人の女性A, B, Cと、4人の男性a, b, c, dがいる状況を考えます。女性たちの男性との知り合い関係は以下のようになっているとします。

• 女性A: 男性a, bと知り合い
• 女性B: 男性a, cと知り合い
• 女性C: 男性aと知り合い

この場合、女性Cは男性aとしか知り合いではありません。つまり、1人の女性を選んだ時に、その女性とその知り合いの男性を合わせても2人しかいません。これは、ホールの結婚定理の条件である「任意のk人の女性（1 ≤ k ≤ n）は、合わせて少なくともk人の男性と知り合いである。」を満たしていません。よって、この状況では全ての女性が異なる男性と結婚できる完全マッチングは存在しません。

3. 安定結婚問題

これまでの章では、マッチング問題と二部グラフにおけるマッチングについて解説し、特に完全マッチングが存在するための条件であるホールの結婚定理を紹介しました。今回の章では、マッチングの安定性という概念を導入し、それぞれの個体が自身の選好に基づいて相手を選ぶ安定結婚問題について解説していきます。さらに、安定結婚問題の解を見つけるためのアルゴリズムとして、Gale-Shapleyアルゴリズムを紹介します。

3.1 安定結婚問題：選好順序に基づくマッチング

安定結婚問題とは、それぞれが異性に対して選好順序を持っている男女集合において、全員が納得できるようなペア（マッチング）を見つける問題です。選好順序とは、各個体が良い順に異性を並べたリストのことです。

安定結婚問題では、単にマッチングを作るだけでなく、ブロッキングペアが存在しないマッチング、すなわち安定マッチングを求めることが重要です。ブロッキングペアとは、現在のマッチングよりも互いに好ましい相手とペアになれる可能性がある2人を指します。

3.2 Gale-Shapley アルゴリズム：安定マッチングを求めるアルゴリズム

Gale-Shapleyアルゴリズムは、安定結婚問題の安定マッチングを効率的に求めるアルゴリズムです。このアルゴリズムは、男性側が女性側にプロポーズを行い、女性側がプロポーズを受け入れるかどうかを決定するというプロセスを繰り返すことで、安定マッチングを導出します。

Gale-Shapleyアルゴリズムの動作は、以下の通りです。

1. 初期状態: 全ての男性と女性はフリーの状態です。
2. プロポーズ: まだプロポーズしていない男性が、自分の選好リストの中で最も順位の高い女性にプロポーズします。
3. プロポーズへの回答: プロポーズを受けた女性は、以下のルールに従って回答します。
   • もし、その女性がフリーであれば、プロポーズを受け入れます。
   • もし、その女性が既に他の男性と婚約している場合は、現在の婚約相手とプロポーズしてきた男性を比較し、より選好順位の高い男性と婚約します。
4. 婚約状態の更新: プロポーズが受け入れられた場合、その男性と女性は婚約状態となります。もし、女性が既に他の男性と婚約していた場合は、以前の婚約は破棄されます。
5. 繰り返し: 全ての男性が婚約するまで、手順2〜4を繰り返します。

Gale-Shapleyアルゴリズムは、有限回のステップで必ず安定マッチングを見つけ出すことが保証されています。

Gale-Shapleyアルゴリズムの例:

具体的な例として、4人の男性 (A, B, C, D) と 4人の女性 (W, X, Y, Z) がいる場合を考えます。それぞれの選好順序は以下の通りとします。

男性:

• A: W > X > Y > Z
• B: X > Y > Z > W
• C: Y > Z > W > X
• D: Z > W > X > Y

女性:

• W: A > B > C > D
• X: B > C > D > A
• Y: C > D > A > B
• Z: D > A > B > C

この例でGale-Shapleyアルゴリズムを実行すると、以下の手順で安定マッチングが得られます。

1. 男性Aが女性Wにプロポーズし、女性Wはプロポーズを受け入れます。(A-W)
2. 男性Bが女性Xにプロポーズし、女性Xはプロポーズを受け入れます。(B-X)
3. 男性Cが女性Yにプロポーズし、女性Yはプロポーズを受け入れます。(C-Y)
4. 男性Dが女性Zにプロポーズし、女性Zはプロポーズを受け入れます。(D-Z)

この時点で、全ての男性が婚約状態になったため、アルゴリズムは終了します。得られたマッチング (A-W, B-X, C-Y, D-Z) は、ブロッキングペアが存在しない安定マッチングです。

Gale-Shapleyアルゴリズムは、安定結婚問題以外にも、研修医の病院配属や臓器移植におけるドナーとレシピエントのマッチングなど、様々な実社会の問題に応用されています。

4. 臨床研修マッチング問題

4.1 研修医配属問題：医学生と病院の安定マッチング

臨床研修マッチングは、研修医と研修病院を互いの希望を考慮しながら最適な形で結びつけるプロセスです。これは、単に研修医を病院に割り振れば良いという単純な問題ではありません。研修医と病院、双方にとって、長期的な視点に立って納得のいくマッチングを実現することが重要になります。

この章では、研修医配属問題を安定結婚問題の拡張として捉え、安定マッチングという概念を軸に解説していきます。安定マッチングとは、マッチング後にも、研修医と病院のどちらにとっても、現状よりも良い条件で組める相手がいない状態を指します。

4.2 安定マッチングは一つとは限らない：研修医に有利なマッチングとは？

Gale-Shapleyアルゴリズムは安定マッチングを見つけ出すアルゴリズムですが、実は安定マッチングは常に一つとは限りません。複数の安定マッチングが存在する場合、研修医と病院、どちらにとって有利なマッチングになるかが問題となります。

臨床研修マッチングにおいては、一般的に研修医側に有利なマッチングが採用されています。これは、研修医が自分自身のキャリアパスを重視し、希望する研修内容や研修環境を選択できるようにするためです。

4.3 1対多マッチングへの対応：病院の定員と研修医の希望

安定結婚問題では、1人の男性と1人の女性がマッチングするという1対1の関係でしたが、臨床研修マッチングは、1つの病院が複数の研修医を受け入れる1対多のマッチングです。この違いに対応するために、Gale-Shapleyアルゴリズムを拡張する必要があります。

具体的には、各病院が受け入れ可能な研修医の数だけ「席」を持っていると見なし、各「席」に対して個別にGale-Shapleyアルゴリズムを適用します。つまり、病院は、研修医の受け入れ枠が許す限り、複数の研修医と「仮マッチング」の状態になることができます。そして、研修医は、複数の病院から「仮マッチング」のオファーを受け、その都度、最も希望順位の高い病院を選びます。このプロセスを繰り返すことで、最終的に安定マッチングが得られます。

4.4 田舎の病院定理：研修医の地方偏在と安定マッチングの関係

臨床研修マッチングでは、「都会の病院に人気が集中し、地方の病院に研修医が行き渡らない」という問題がしばしば指摘されます。これを説明する上で重要な概念が、「田舎の病院定理」です。

田舎の病院定理は、研修医の選好が病院の地理的な条件に大きく影響される場合、研修医に有利な安定マッチングにおいて、地方の病院は、希望する研修医を必ず確保できることを示しています。

例:

ある研修医が、都会の病院よりも、実家近くの地方の病院を強く希望しているとします。この研修医は、都会の病院から「仮マッチング」のオファーを受けても、それを断り、実家近くの病院からのオファーを待つ可能性があります。なぜなら、Gale-Shapleyアルゴリズムは、研修医にとって最適な安定マッチングを保証しているため、希望順位の低い都会の病院と「仮マッチング」してしまうと、後で希望順位の高い地方の病院からオファーが来た際に、そちらとマッチングできなくなるリスクがあるからです。

4.5 耐戦略性：正直であることの重要性

Gale-Shapleyアルゴリズムに基づく臨床研修マッチングは、耐戦略性という重要な性質を持っています。耐戦略性とは、研修医と病院のいずれも、自身の希望を偽って伝えることによって、自分にとってより有利な結果を得ることができないという性質を指します。

言い換えれば、このマッチングシステムでは、嘘をついたり、駆け引きをしたりするメリットがありません。 研修医が、本当は第一希望ではない病院を、早くマッチングを決めたいという理由で第一希望と偽ったり、病院側が、本当は採用したい研修医ではない人物を、他の病院に取られてしまうことを恐れて採用枠を埋めるために採用したりといった行為は、最終的には自分たちに不利な結果をもたらす可能性があります。

なぜなら、Gale-Shapleyアルゴリズムは、全ての参加者が正直に希望を表明することを前提に、安定マッチングを導き出すように設計されているからです。 研修医、病院のいずれかが戦略的に行動した場合、アルゴリズムの前提が崩れ、最終的なマッチングが安定マッチングではなくなる可能性があります。その結果、希望していない病院に配属されたり、希望する研修医を採用できなかったりする可能性が出てきてしまいます。

臨床研修マッチングにおいては、研修医も病院も、正直に、自分の希望する条件や人材を伝えることが、最善の結果に繋がるということです。

4.6 プロジェクトマネジメントの観点からのタスク分担：スキルと希望の一致

このブログ記事の前に、プロジェクトマネジメントに関する記事を掲載する予定とのことですが、臨床研修マッチングは、プロジェクトチームを編成するプロセスにも類似していると言えます。

プロジェクトマネジメントにおいては、タスクの分担を各メンバーのスキルに応じて行うことが重要です。同様に、臨床研修マッチングにおいても、病院は、研修医のスキルや経験を考慮しながら、適切な研修計画を立てる必要があります。

さらに、プロジェクトマネジメントにおいては、メンバーのモチベーションを高めるために、各メンバーの希望するタスクや役割を考慮することも重要です。同様に、臨床研修マッチングにおいても、研修医の希望する専門分野やキャリアパスを考慮することで、研修医のモチベーションを高め、より効果的な研修を実現することができます。

まとめ：プロジェクトマネジメントとマッチングシステムの重要性

この章では、臨床研修マッチング問題を通じて、プロジェクトマネジメントの手法とマッチングシステムの重要性について解説しました。特に、Gale-Shapleyアルゴリズムを用いた安定マッチングの概念は、研修医と病院の双方にとって最適な結果を導くための強力なツールであることが示されました。

プロジェクトマネジメントにおいては、リソースの最適化やタスクの効率的な分担が求められます。マッチングシステムは、各メンバーのスキルや希望を考慮し、最適なタスク配分を実現するための有効な手段です。これにより、チーム全体のパフォーマンスを向上させ、プロジェクトの成功確率を高めることが可能となります